op-amp + RLC 발진기 (간단한 예제) 해석

 

 

 

 

 

 

 

루프 이득을 구하는 방법

 

(갑자기 루프? 정귀환 없이 혼자서 발산하는 시스템이 얼마나 되겠는가... 발진을 위해 정귀환을 사용하는 것은 자연스러운 발상이다.)

 

입력이 0인 폐루프 시스템으로 해석 가능하다.

입력이 0인 폐루프 시스템의 루프이득을 구하는 과정은 다음과 같다.

 

1. $V_o$에서 회로를 오픈한다.

2. 입력을 0으로 준다.

3. $V_o$에서 $V_r$ 까지의 이득을 구한다.

 

 

그리고 이를 블록선도와 같이 보면 이해가 편한데, 다음과 같다.

 

 

루프 이득을 구하는 다른 방법

 

폐루프 시스템의 루프 이득을 구하는 다른 방법은 $V_o$에서 출발하지 않고 $V_i$에서 출발하는 것이다.

과정은 다음과 같다.

 

1. $V_r$을 오픈한다.

2. $V_i$에서 $V_r$ 까지의 이득을 구한다.

 

회로와 블록선도는 다음과 같다.

 

 

 

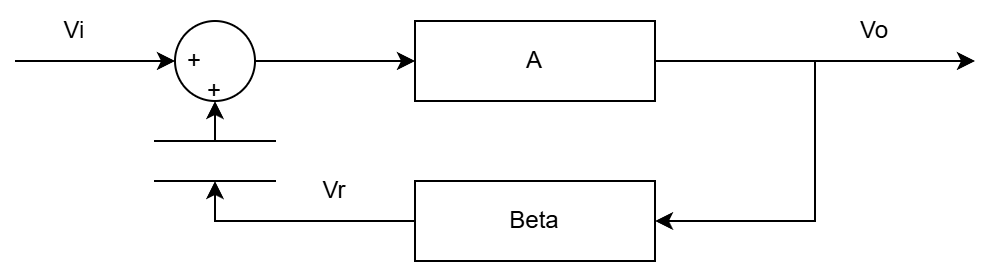
루프 이득 분석

위의 두 방법 중 하나로 루프 이득을 구해보면 다음과 같다.

$$A(s)\beta(s) = \frac {s \frac 1 {RC} (1 + \frac {r_2} {r_1})} {s^2 + s \frac 1 {RC} + \frac 1 {LC}}$$

 

방법1

안정성 판정을 위해 특정 주파수에서의 이득을 구해보면

$$A(jw)\beta (jw) = \frac {j \frac w {RC} (1 + \frac {r_2} {r_1})} {(-w^2 + \frac 1 {LC}) + j \frac w {RC}}$$

$w_0 = \frac 1 {\sqrt {LC}}$에서 루프 이득이 $1 + \frac {r_2} {r_1}$ $\rightarrow$ 임계 안정 (불안정 직전)이 됨을 알 수 있다.

왜냐하면 루프 이득이 1이라는 것은 phase가 $0^\circ$인 곳에서의 이득인데, 이것이 1보다 크면 nyquist 선도 상에서 1을 포함해서 한바퀴를 돌기 때문이다. (이것이 이해가 안간다면 nyquist 선도를 통한 안정도 판별에 대해 공부해보길 바란다. 시스템의 안정도를 산출하는데에 우방평면 상의 극점의 정확한 위치가 항상 필요한 것은 아니다. https://akswnd98.tistory.com/52)

발진기에서는 의도적으로 불안정성을 유도해야 하므로, $\frac {r_2} {r_1} > 0$. 보통은 $w_0$에서의 루프 이득이 2 정도 되게 끔 설계한다.

 

정리하면 다음과 같다.

루프이득의 phase가 $0^\circ$가 되는 $w_0$가 왠만하면 존재할 텐데, 그 루프 이득 값 ( = 실수이다. 왜냐하면 phase가 0도 이기 때문)이 1이상이 되야한다는 것이다.

 

방법2

정귀환 폐루프 시스템의 극점을 조사해본다.

정귀환 폐루프 시스템 전달함수 = $\frac A {1 - A(s)\beta (s)}$이므로 $1 - A(s)\beta(s)$의 분자를 조사해본다.

정리해보면 다음과 같다.

$$(s - \frac 1 2 \frac 1 {RC} \frac {r_2} {r_1})^2 + \frac 1 {LC} - (\frac 1 2 \frac 1 {RC} \frac {r_2} {r_1})^2$$

이는 $(s - a)^2 + w_{00}^2$ (a는 양수) 이므로 지수적으로 발산하는 정현파를 떠올릴 수 있다.

여기서 $w_{00} \neq w_0$인데 $(\frac 1 2 \frac 1 {RC} \frac {r_2} {r_1})^2$가 크지 않다면 그 차이는 크지 않음을 알 수 있다.

 

 

후처리 (비선형 회로)

진폭이 발산하면 안되기 때문에 특정 진폭에 도달했을 때 비선형 회로를 통해 $w_0$를 정확히 1로 수렴하도록 만든다.

리미터 회로를 사용하는 방법 ($\rightarrow$ 진폭을 강제로 리미팅)

과 제어 가능 저항 소자 (JFET, 다이오드)를 귀환 루프에 놓는 방법 ($\rightarrow$ 진폭이 커지면 이득이 작아짐)

이 사용된다.